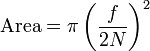Il numero f viene utilizzato per esprimere la quantità di luce che un obiettivo può catturare, quindi 85 mm f / 1.8 e 24 mm f / 1.8 possono catturare la stessa quantità. Qui, f è la lunghezza focale ef / 1.8 significa che il diametro massimo di apertura è di 47,2 mm nel primo esempio e 13,3 mm nel secondo.

Quello che devi considerare qui è che l'obiettivo da 85 mm ha un campo visivo molto più stretto, quindi deve raccogliere la stessa quantità di luce da un'area molto più piccola - per compensare la vista ristretta, l'apertura deve essere maggiore.

Di quanto il l'apertura deve essere maggiore è correlata linearmente alla lunghezza focale. Potremmo dire che un obiettivo da 24 mm con apertura di 13,3 mm può raccogliere tanta luce quanto un obiettivo da 85 mm con apertura di 47,2 mm, ma parlare del numero F lo rende molto più facile da notare.

La terminologia è confusa, vero?

Il numero f / di un obiettivo f / 1.8 è semplicemente 1.8 . Questo è dato da N , non da f . f è la lunghezza focale.

f / 1.8 significa letteralmente "lunghezza focale divisa per N ". Quindi, se ti riferisci af / 1.8, questo non è il numero f, è la lunghezza focale divisa per il numero f.

Per spiegare ulteriormente le equazioni:

La seconda equazione dice che la lunghezza focale f divisa per il diametro dell'apertura d è il numero f N . Oppure f / N = d . Quindi f / 1,8 significa letteralmente "lunghezza focale divisa per 1,8 (uguale al diametro).

Se osservi l'equazione in alto poiché f / N = d , allora f / 2N deve essere d / 2 (e d / 2 è la metà del diametro, così come il raggio dell'apertura). E sappiamo che l'area di un cerchio è pi r quadrato . Quindi pi per f / 2N quadrato è semplicemente l'area dell'apertura dell'apertura.

Quindi un'equazione ti dice il diametro dell'apertura dell'apertura e l'altra utilizza la geometria di base per calcolare l ' area dell'apertura dell'apertura, che è un cerchio.

Penso che la confusione derivi da due cose diverse che le spiegazioni erroneamente raggruppano insieme come "quantità di luce".

La vera quantità di luce che un obiettivo lascia entrare è solo una funzione dell'area di apertura. Poiché l'area va con il diametro al quadrato, questo è proporzionale al quadrato del diametro.

Tuttavia, ciò che è più rilevante per l'esposizione non è la quantità totale di luce che un obiettivo può raccogliere, ma la luminosità dell'immagine a fuoco che produce. È qui che entra in gioco la lunghezza focale. Supponiamo che tu abbia un obiettivo da 100 mm con un'apertura di 25 mm di diametro (o un'apertura regolabile impostata su 25 mm). Ora confrontalo con un obiettivo da 200 mm. Se l'obiettivo da 200 mm ha anche un'apertura di 25 mm, lascerà entrare la stessa quantità di luce. Tuttavia, la stessa quantità di luce proveniente dal soggetto viene ora messa a fuoco due volte più grande, occupando quindi 4 volte l'area. Ciò significa che l'obiettivo da 200 mm con apertura di 25 mm crea un'immagine 1/4 più luminosa (2 f-stop in basso) rispetto all'obiettivo da 100 mm con la stessa apertura di 25 mm.

Si noti che la luminosità di l'immagine a fuoco scende con il quadrato della lunghezza focale, ma sale con il quadrato del diametro dell'apertura. Ciò significa che se dovessimo prendere il rapporto tra i due, otterremmo una misura normalizzata di quanto sarà luminosa l'immagine a fuoco ai fini dell'esposizione. Quel rapporto è esattamente ciò che sono f-stop. Questi sono comunemente scritti come f / n, come f / 8.0 of / 11 per esempio. Questa è solo un'espressione. L'equazione completa è:

  aperture = focallength / n  

Nel primo esempio di obiettivo da 100 mm con apertura di 25 mm, ovvero:

  25mm = 100mm / 4  

Dal momento che diventa ingombrante scrivere e dire tutto il tempo e il punto è non doversi preoccupare della lunghezza focale e dell'apertura assolute sono, questo è abbreviato in "f / 4", con "f" che si riferisce alla lunghezza focale dell'obiettivo e "4" è il rapporto tra quella lunghezza focale e il diametro dell'apertura. Il secondo esempio era:

  25 mm = 200 mm / 8

o "f / 8". Oltre a piccole perdite di luce e altri effetti sottili che puoi ignorare la maggior parte del tempo, un obiettivo con l'apertura impostata su f / 8 creerà la stessa immagine focalizzata sulla luminosità di un altro obiettivo af / 8 indipendentemente dalla lunghezza focale. Questo spiega anche perché le lenti lunghe tendono ad avere un diametro maggiore. Un obiettivo da 50 mm richiede solo un'apertura di 12,5 mm per ottenere f / 4. Un obiettivo da 300 mm d'altra parte richiede un'apertura di 75 mm di diametro per ottenere la stessa luminosità dell'immagine dello stesso soggetto. Ciò significa che la fisica di base dice che un obiettivo da 300 mm deve avere un diametro di almeno 3 pollici in qualche modo per ottenere f / 4.

Che cosa significa f nei valori f-stop

f sta per la lunghezza focale dell'obiettivo. Un obiettivo f / 1.8 ha il diametro della pupilla d'ingresso di D = f / 1.8. Un obiettivo da 85 mm con apertura f / 1.8 avrà il diametro della pupilla d'ingresso di 85 / 1.8 = 47,2 mm. Una lente da 24 mm avrà il diametro della pupilla di 24 / 1,8 = 13,3 mm. Poiché la quantità di luce che passa attraverso la lente è proporzionale all'area della pupilla d'ingresso e quest'ultima è proporzionale al quadrato del suo diametro, apparentemente l'obiettivo da 85 mm raccoglierà

(47.2 / 13.3) ^ 2 = (85/24) ^ 2 = 12,5

volte più luce. Tuttavia, questa considerazione è vera solo per la quantità di luce, raccolta da ogni singolo punto dell'oggetto, non per la quantità totale di luce proveniente dallo spazio dell'oggetto.

Stessa f -numero, stessa esposizione (indipendente da f o D)

Una cosa che ho anche trovato confusa è che la quantità di luce raccolta a il sensore con la stessa velocità dell'otturatore di obiettivi diversi con lo stesso numero f è lo stesso. Come mai se un obiettivo è chiaramente più grande dell'altro?

Ecco un'illustrazione di ciò che accade nella fotocamera:

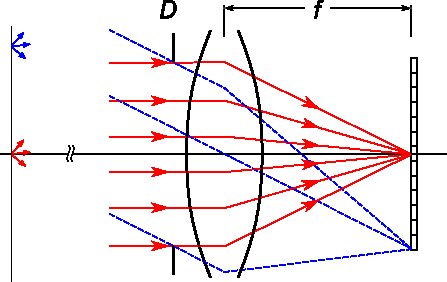
Per semplicità, si presume che l'oggetto sia all'infinito, in modo che tutti i raggi dallo stesso punto dell'oggetto siano paralleli tra loro. I raggi rossi solidi entrano nella lente parallelamente al suo asse e sono tutti focalizzati al centro dell'inquadratura. I raggi blu tratteggiati sono paralleli tra loro ma non paralleli all'asse. Si concentrano tutti sul bordo del fotogramma. Pertanto, la dimensione del fotogramma insieme alla distanza focale dell'obiettivo determinano il campo visivo dell'obiettivo.

(Nota che poiché ho reso infinita la distanza dell'oggetto, il campo visivo nello spazio dell'oggetto è un angolare.)

Se cambiamo l'obiettivo con uno con una lunghezza focale maggiore mantenendo le stesse dimensioni del fotogramma, il campo visivo dell'obiettivo diminuisce:

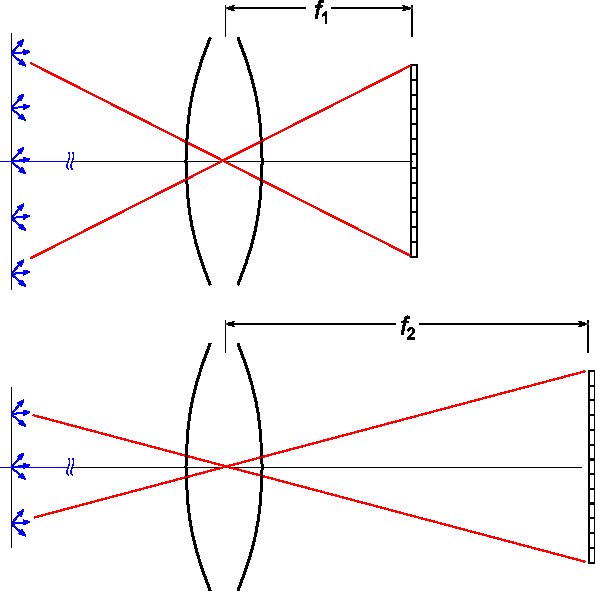
Pertanto, mentre l'obiettivo raccoglie ancora la stessa quantità di luce da ogni punto nello spazio dell'oggetto, la dimensione di questo spazio è minore, quindi la quantità totale di luce che raggiunge la pellicola o il rilevatore è ridotta .

Questa riduzione è proporzionale all'aumento della lunghezza focale, ovvero la quantità di luce con lo stesso D viene ridotta di un fattore (f2 / f1) ^ 2. (È al quadrato perché dobbiamo tenere conto della riduzione del campo visivo in entrambe le direzioni.)

Se ora aumentiamo D di f2 / f1, lo faremo di nuovo raccogliere la vecchia quantità di luce (poiché è proporzionale a D ^ 2). Il numero f diventerà: D2 / f2 = [D1 * (f2 / f1)] / f2 = D1 / f1. Quindi, se vogliamo raccogliere la stessa quantità di luce cambiando la lunghezza focale, dobbiamo mantenere costante il numero f.

La dimensione del fotogramma è importante

L'ultimo parametro di interesse è la dimensione del frame. Prendi una fotocamera compatta con lo stesso obiettivo con numero f di una SLR full-frame. Se le dimensioni sia dell'obiettivo che del sensore vengono ridotte proporzionalmente alla lunghezza focale, le due telecamere avranno lo stesso campo visivo. La fotocamera compatta raccoglierà meno luce rispetto alla SLR perché il suo obiettivo è più piccolo. Tuttavia, fornirà comunque lo stesso valore di esposizione sul sensore perché l'esposizione è la quantità di luce per unità di area .

Se le due fotocamere hanno la stessa risoluzione, l'esposizione sarà la stessa ma la quantità effettiva di luce su ciascun pixel sarà maggiore con la fotocamera SLR più grande, con conseguente riduzione del rumore.

Qualsiasi obiettivo af / 2.8 dovrebbe fornire la stessa quantità di luce alla fotocamera. Alcuni obiettivi devono lavorare di più per arrivarci.

Non è tecnicamente accurato, ma ho scoperto che il modo migliore per capire il numero di f-stop è anche pensare che rappresenti la quantità di luce perduto. Quindi af / 2.8 stai perdendo solo 2,8 volte la quantità di luce, mentre af / 11 stai perdendo 11 volte la quantità di luce. *

Un teleobiettivo, per sua natura, ha a che fare con meno luce di un obiettivo grandangolare. Quindi più l'obiettivo deve lavorare per evitare di perdere luce, più vetro è necessario per catturare quanta più luce possibile, quindi puoi avere un 55-250 f / 4-5.6 che pesa circa 1 libbra ed è 6-8 pollici, mentre un 70-200mm f / 2.8 pesa 6 libbre ed è lungo oltre 12 pollici.

* Questo non è il modo in cui funziona da un punto di vista matematico, ma può aiutarti con una comprensione pratica del lavoro.