L'equazione presuppone una semplice lente a elemento singolo che sia bilateralmente simmetrica. L'obiettivo della fotocamera, per mitigare le 7 principali aberrazioni (carenze che si degradano) è costruito utilizzando diversi elementi di lenti in vetro individuali. Alcuni hanno un potere positivo, altri un potere negativo. Alcuni sono distanziati in aria e alcuni sono cementati insieme. Poiché questa matrice diventa piuttosto complessa, il punto da cui misuriamo la lunghezza focale verrà probabilmente spostato dal centro fisico del barilotto dell'obiettivo.

In un vero teleobiettivo, il nodale posteriore (punto di misurazione) è spostato in avanti. Questa azione accorcia la lunghezza del barilotto dell'obiettivo, rendendo la fotocamera e l'obiettivo meno scomode da tenere, utilizzare e riporre. In alcuni modelli, il nodale posteriore può effettivamente cadere in aria davanti al barilotto dell'obiettivo.

Come afferma l'equazione: all'unità (ingrandimento 1), la distanza del soggetto è di 2 lunghezze focali in avanti e il fuoco posteriore è di 2 lunghezze focali dietro il nodale posteriore. Il problema è che non puoi individuare facilmente il nodale posteriore. Tuttavia, una volta ottenuto l'ingrandimento 1, è ora possibile misurare la distanza tra soggetto e immagine. Molte fotocamere forniscono un simbolo (cerchio diviso in due da una linea) sulla cornice della fotocamera; per individuare la posizione del piano dell'immagine.

In ogni caso, misurare la distanza da soggetto a immagine e dividerla per 4. Questa divisione rivela la lunghezza focale. Dividi per 2 e questa divisione individua il punto nodale posteriore. Ora sei meglio equipaggiato per utilizzare la "formula del produttore di lenti".

prima di tutto, complimenti per il tuo sforzo di scomporre un problema di fotografia in base ai principi fondamentali.

La discrepanza che hai osservato deriva da una comune semplificazione eccessiva. Il tuo obiettivo da 100 mm è in realtà ciò che gli ingegneri ottici chiamano un "gruppo di lenti" Come probabilmente saprai, è composto da più lenti elementi in gruppi che lavorano in tandem per formare, perfezionare e trasmettere l'immagine vista dal sensore di immagine.

Se il tuo gruppo obiettivo da 100 mm fosse costituito da un singolo elemento dell'obiettivo da 100 mm, avresti enormi distorsioni e solo il rosso, il verde o il blu potrebbero essere a fuoco alla volta, ma il sottile l'equazione di ingrandimento dell'obiettivo che avresti collegato sarebbe rimasta vera. Un ingrandimento di 1 si ottiene quando il soggetto è a 200 mm dal punto nodale e il gruppo dell'obiettivo deve essere fisicamente maggiore di 200 mm di lunghezza. Anche allora, questo sarebbe strettamente accurato solo nella misura in cui l'equazione della lente sottile è appropriata (e non è particolarmente appropriata qui). Una risposta corretta verrebbe da una derivazione del produttore di lenti equazione

Un corollario della differenza tra un assieme e una lente sottile sono i punti nodali bilocati. Una lente sottile ha un'unica posizione per i punti nodali anteriori e posteriori; Entrambi sono collocati con l'allievo d'ingresso. Se questo fosse vero per il tuo gruppo obiettivo, saresti in grado di liberare l'obiettivo ruotando attorno all'apertura dell'obiettivo senza alcuna parallasse al soggetto o al sensore. Sono sicuro che se lo provassi con il 100mm macro scopriresti che non è vero. Una lente spessa ha due punti nodali che sono collocati solo se il suo indice netto è 0, I.E. non ha lunghezza focale. Un gruppo di lenti può essere approssimato da una lente spessa virtuale con due indici idealizzati in modo tale che la lente virtuale abbia gli stessi vertici, lunghezze focali relative, pupilla d'ingresso e punti nodali (salienti) del gruppo di lenti.

Per ulteriore credito, potresti controllare la descrizione di un obiettivo composto e provare a indovinare quali combinazioni di lunghezze focali dell'obiettivo creerebbero la situazione che hai descritto. NB l '"ingrandimento del telescopio". Questo è essenzialmente ciò che fa un progettista di obiettivi.

Per ulteriori letture puoi dare un'occhiata ai diversi tipi di design di obiettivi fotografici

La maggior parte degli obiettivi a lunghezza focale fissa mette a fuoco modificando la lunghezza focale oltre a spostare i punti nodali dell'obiettivo. Per mettere a fuoco un oggetto vicino alla fotocamera, l'obiettivo riduce la sua lunghezza focale. Un obiettivo specificato come "100 mm" di solito è "100 mm quando messo a fuoco all'infinito", ma non necessariamente quando è messo a fuoco su un oggetto vicino.

Ci sono due ragioni per cui la distanza del soggetto dall'immagine non è di 40 cm con un ingrandimento unitario:

1. la lunghezza focale dell'obiettivo potrebbe non essere di 100 mm
2. la distanza tra i piani principali potrebbe non essere zero.

Quale di questi motivi sia il più importante è impossibile da dire senza informazioni dettagliate sul design ottico dell'obiettivo.

Lunghezza focale

Il valore "100 mm" scritto sulla lente stessa è una distanza focale nominale , che normalmente è un valore arrotondato della focale reale distanzaquando l'obiettivo è messo a fuoco all'infinito.

Alcuni obiettivi, solitamente chiamati obiettivi di "focalizzazione dell'unità", raggiungono la messa a fuoco spostando il gruppo ottico nel suo insieme. Queste lenti hanno una distanza focale che non varia con la messa a fuoco. Tuttavia, molti obiettivi complessi, incluso praticamente qualsiasi obiettivo macro moderno, hanno una sorta di "correzione della distanza ravvicinata" (nel gergo Nikon): la loro formula ottica cambia durante la messa a fuoco, il che consente una migliore correzione delle aberrazioni. Questi obiettivi hanno una distanza focale che ti concentri.

Questi due fatti: l'arrotondamento della lunghezza focale nominale e il fatto che varia quando metti a fuoco, significano che non sai quale sia la lunghezza focale effettiva dell'obiettivo con ingrandimento unitario.

Piani principali

La pagina di Wikipedia che citi definisce d _o ed _i come la distanza dalla lente all'oggetto (risp. immagine ), ma nota che queste definizioni vengono visualizzate in una sezione che riguarda specificamente le lenti sottili. Poiché la lente è una lente composta spessa, questo solleva la questione dell'applicabilità della formula.

Si scopre che l'approssimazione della lente sottile non è applicabile in questa situazione. Tuttavia, la formula è ancora valida se interpretata nel contesto del modello lente spessa . In questo modello, il piano della lente sottile è sostituito da due piani, chiamati "piani principali":

• il "frontale" (o "primario", o "Lato oggetto") viene utilizzato il piano principale per misurare le distanze nello spazio dell'oggetto
• il piano principale "posteriore" (o "secondario" o "lato immagine") viene utilizzato per misurare le distanze nello spazio dell'immagine

Questi sono piani coniugati con ingrandimento unitario. Nella figura sotto ( sorgente), sono i piani verticali che passano per H ₁ , N ₁ e H _{2 sub >, N 2 :}

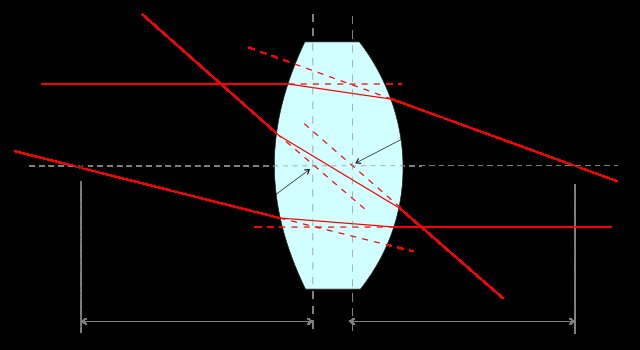
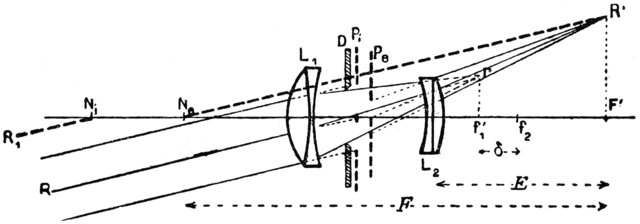
Notare che questo modo di descrivere un sistema ottico in termini di punti cardinali (la F _i , H _i e N _i sopra) è applicabile anche alle lenti composte. Vedi ad esempio questo vecchio disegno di un teleobiettivo ( fonte) dove entrambi i piani principali (i piani verticali attraverso N _i e N _o ) sono a sinistra lato dell'elemento più a sinistra:

Pertanto, la tua formula è ancora valida a condizione che tu definisca:

• d _{o come distanza dal soggetto al piano principale primario}
• d _i come distanza dal piano principale secondario all'immagine

Ciò fornisce la distanza dal soggetto all'immagine come

d _o + e + d _i = 4f + e

all'ingrandimento unitario, dove e è la distanza (possibilmente negativa) tra i piani principali. Nota che l'approssimazione della lente sottile dice essenzialmente che i piani principali sono coincidenti (e = 0), ma non è applicabile al tuo caso.

Per maggiori informazioni su questo argomento, puoi dare un'occhiata a:

• questo breve video sugli aerei principali
• queste dispense sulle lenti spesse

L'idea sbagliata dell'obiettivo sottile

Ho scritto questa risposta principalmente per aiutare a chiarire un malinteso popolare, che appare in alcune delle risposte qui, inclusa quella che hai accettato: che un obiettivo fotografico è equivalente a un obiettivo sottile .

Si scopre che nella maggior parte delle situazioni fotografiche (praticamente tutte le situazioni non macro), la distanza dal soggetto all'obiettivo è molto maggiore di qualsiasi distanza caratteristica dell'obiettivo stesso. In tali situazioni non importa quale punto di riferimento usi per misurare la distanza dal soggetto. È quindi conveniente dimenticare la distanza che separa i piani principali e considerare che il piano posteriore principale è l'unico che conta. Ciò equivale a impostare e = 0, che è fondamentalmente l'approssimazione della lente sottile.

Attenersi a questa approssimazione rende l'apprendimento dell'ottica molto più semplice, poiché non è necessario comprendere nozioni come piani principali, punti principali o punti nodali , spazio oggetto, spazio immagine e così via. Considerando che:

• l'approssimazione è abbastanza buona per la maggior parte scopi (non macro)
• la conoscenza dell'ottica è utile solo per un fotografo in un livello qualitativo, dato che non progetterai obiettivi e non avrai bisogno di esperienza ottica per diventare un grande fotografo

è comprensibile che l'obiettivo sottile sia il modello più comunemente insegnato ai fotografi. Eppure l'approssimazione si interrompe quando si ha a che fare con un obiettivo spesso complesso a macro distanze. Le risposte che ti dicono che la distanza focale è un quarto della distanza dal soggetto all'immagine illustrano come questo malinteso induca le persone a pubblicare risposte sbagliate.

La distanza di lavoro viene misurata dalla parte anteriore dell'obiettivo al soggetto. Per l'obiettivo macro EF 100 mm f / 2,8 L IS USM, la distanza di lavoro alla distanza minima di messa a fuoco (MFD) / ingrandimento completo è di circa 133 mm.

La distanza di messa a fuoco viene misurata dal soggetto al piano di imaging (pellicola o sensore). Per l'obiettivo EF 100 mm f / 2.8 L IS USM Macro, la distanza di messa a fuoco a pieno ingrandimento / MFD è di 300 mm.

La maggior parte delle lunghezze focali vengono misurate quando l'obiettivo è messo a fuoco all'infinito (e quindi arrotondato al lunghezza focale "standard" più vicina). Quando la distanza di messa a fuoco si riduce, l'angolo di campo fornito dall'obiettivo spesso cambia. Questo è ciò che è noto come respiro focalizzato . L'MFD da 300 mm del tuo EF 100 mm f / 2.8 L IS USM Macro ci rivela che la lunghezza focale effettiva con ingrandimento 1: 1 è di circa 75 mm. Questo è abbastanza comune per un obiettivo Macro con lunghezza focale compresa tra 90 e 105 mm. Il Tamron 90mm f / 2.8 Di VC USD Macro (F017), ad esempio, ha anche un MFD di 300 mm con ingrandimento 1: 1.

Inoltre, la lunghezza focale di un obiettivo composto è approssimata dalla lunghezza focale una singola lente dovrebbe fornire la stessa quantità di ingrandimento. Una lente composta è un sistema di più lenti, solitamente disposte in gruppi, che insieme agiscono come una singola lente. Quasi tutti gli obiettivi disponibili in commercio per i sistemi di telecamere con obiettivi intercambiabili sono obiettivi composti. Il tuo EF 100 mm f / 2.8 L IS Macro ha 15 elementi dell'obiettivo disposti in 12 gruppi.

Per la maggior parte degli obiettivi grandangolari con design retrofocus, questo semplice punto teorico dell'obiettivo singolo è ben dietro la parte anteriore dell'obiettivo . Per i teleobiettivi questo punto è, per definizione, davanti alla parte anteriore dell'obiettivo.

Quando messo a fuoco alla distanza minima di messa a fuoco (MFD) di 300 mm, la parte anteriore del tuo EF 100 mm f / 2.8 L IS USM Macro si trova a circa 168 mm davanti al sensore. Ma il campo visivo e l'ingrandimento forniti dall'obiettivo su MFD lo rendono effettivamente un obiettivo da 75 mm a quella distanza di messa a fuoco. Ciò significa che un semplice obiettivo da 75 mm dovrebbe trovarsi a 150 mm davanti al sensore (che lo posiziona anche a 150 mm dal soggetto) per un ingrandimento 1: 1. Questo posiziona il punto centrale effettivo del tuo EF 100 mm f / 2.8 Macro a circa 18 mm dietro la parte anteriore dell'obiettivo quando messo a fuoco sull'MFD.

Quindi penso che mi manchi qualcosa, qualcuno può spiegare dove mi trovo Sbaglio?

Quando applichi formule come quelle nella tua domanda, devi usare 75 mm per la lunghezza focale dell'obiettivo quando è messo a fuoco su MFD.