La tua intuizione è giusta. Per convalidarlo, possiamo scavare nella geometria di base delle scuole superiori.

Sebbene l'obiettivo di una fotocamera sia in realtà un obiettivo complesso composto da molti elementi, concettualmente e matematicamente per scopi pratici, questo si riduce ad un ideale, dove si può immaginare un foro stenopeico esattamente ad una distanza dal sensore pari alla focale. La luce potrebbe cadere al di fuori del cono, ma non ci interessa poiché non verrà registrata, quindi l'angolo di quel cono è l ' angolo di campo.

Quindi, la geometria del liceo, in arrivo. Ecco un diagramma idealizzato che mostra le lunghezze focali di 35 mm e 70 mm (immagina una vista dall'alto verso il basso):

La prima cosa da notare è che per confrontare simili è necessario misurare la distanza dal "foro di spillo", non dal sensore. Ma, poiché normalmente lavori a distanze di metri invece che di millimetri, questo è normalmente trascurabile e non vale la pena preoccuparsi.In questo diagramma, ho mantenuto il foro stenopeico dell'obiettivo nello stesso punto e ho spostato il sensore per ingrandire.

La linea grigia a destra rappresenta la nostra distanza dal soggetto, a 6 cm. Ovviamente, 6 m potrebbe essere una distanza non macro più tipica, e su quella scala la differenza tra l'allineamento del sensore o della fotocamera nel suo insieme e il centro nominale dell'obiettivo non ha importanza ; qui lo fa, ma questo è il prezzo che paghiamo per un diagramma che mostra i dettagli e che si adattano a uno schermo.

L'importante è che il campo visivo sia una questione di " triangoli simili ". Considera il triangolo ∆CDE , quello che ottieni con un obiettivo da 35 mm. Il triangolo ∆FHE ha gli stessi angoli: la dimensione è diversa ed è ovviamente riflessa, ma possiamo vedere che gli angoli sono gli stessi. Ecco quei gruppi di triangoli ombreggiati per chiarezza:

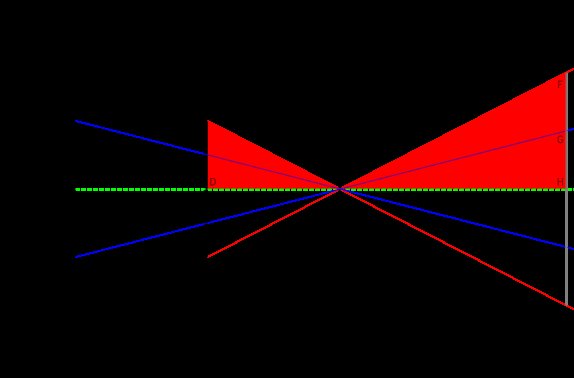
e quelli corrispondenti a 70 mm:

Sto mostrando solo metà del fotogramma perché è più facile pensare ai triangoli rettangoli, ma questo vale anche se aggiungi la metà inferiore per creare triangoli isosceli che mostrano l'intero angolo di visuale. (Con me, ancora?)

Quindi, la domanda fondamentalmente è: mentre spostiamo la lunghezza focale da DE a BE , cosa succede alla linea corrispondente in FH → GH ? Possiamo vedere dalla costruzione che quando raddoppiamo la lunghezza focale, la linea del campo visivo grigio si dimezza, il che supporta la tua conclusione intuitiva.

Possiamo anche eseguire il backup di questo con la matematica; potremmo capire gli angoli, ma penso che il modo più intuitivo sia ragionare sui triangoli simili: ricorda, la regola è che i lati di questi triangoli sono proporzionali tra loro.

Ciò significa CD / DE = FH / EH . Se raddoppiamo DE , moltiplichiamo un lato dell'equazione per ½. Dobbiamo moltiplicare anche l'altro lato per lo stesso importo per mantenere la proporzione, quindi CD / 2 × DE = FH / 2 × EH - ma non siamo interessati a cambiare EH in questo caso (stiamo mantenendo il soggetto alla stessa distanza), quindi possiamo invertirlo: CD / 2 × DE = ½FH / EH .

Ora, guardando indietro al diagramma , 2 × DE è uguale a BE (perché DE è 35 mm e BE è 70 mm), quindi CD / BE = ½FH / EH . Sappiamo anche che AB è esattamente uguale a CD (perché la dimensione del sensore è la stessa), quindi AB / BE = ½FH / EH .

E , guardando i triangoli blu, sappiamo che AB / BE = GH / EH . Quindi, poiché ½FH / EH e GH / EH sono entrambi uguali a AB / BE , possiamo dire che GH / EH = ½FH / EH , che semplifica in GH = ½FH - rispondendo matematicamente alla domanda sopra .

E, ricorda, che ½ è perché abbiamo raddoppiato la lunghezza focale - proviene da 35mm ÷ 70mm . Quindi, la formula si generalizza a vecchio ÷ nuovo per qualsiasi modifica della lunghezza focale.

A volte, le persone confondersi perché l'angolo ∠FEH (o ∠GEH ) come valore in gradi non scala linearmente - sembra che lo faccia a lunghe lunghezze focali ma divergente per quelli molto brevi. Ma, se lo segui fino alla larghezza o all'altezza della cornice a una certa distanza, scoprirai che quella scalatura segue la stessa semplice matematica dappertutto. Non è poi così complicato; è solo la natura delle tangenti.

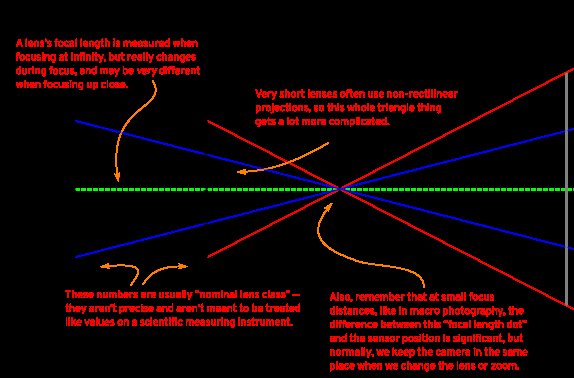
Naturalmente, questo è tutto nel senso ideale. Nel mondo reale, ci sono alcuni avvertimenti:

• Primo, a distanze di messa a fuoco molto ravvicinate (distanza macro), la differenza tra "distanza dal sensore" e "distanza dalla lunghezza focale dell'obiettivo" è importante ;
• secondo, nel mondo reale, la messa a fuoco modifica in una certa misura la lunghezza focale della maggior parte degli obiettivi, quindi nulla è perfettamente ideale; e
• terzo, quando arrivi agli estremi come il tuo esempio di obiettivo da 1 mm, è difficile ottenere una proiezione rettilinea quindi ... tutte le ipotesi sono sbagliate. E, anche per obiettivi normali, la proiezione non è esattamente perfetta; ci saranno distorsioni che influenzano leggermente questo aspetto.

Oh, e un ulteriore avvertimento: se stai cercando di usarlo per la misurazione, probabilmente non dovresti, perché gli obiettivi progettati per la fotografia sono non è etichettato con precisione e può variare dal valore nominale del 10% o più senza che nessuno ci pensi.

Ma, agitando la mano A parte queste cose, la cosa importante è: sì, la quantità di inquadratura riempita da un soggetto di una certa dimensione a una certa distanza raddoppia quando raddoppi la lunghezza focale .

Oppure per in altre parole, lo zoom idealizzato è matematicamente indistinguibile dal ritaglio e dall'ingrandimento idealizzati.

Non è esattamente vero, ma è una prima approssimazione e abbastanza buono per molti scopi pratici.

Consideriamo un ideale obiettivo sottile. Stiamo già introducendo un livello di errori, perché gli obiettivi reali non sono l'ideale, ma dobbiamo iniziare da qualche parte. L'equazione della lente sottile è

dove f è la lunghezza focale, s è la distanza dal soggetto e o è la distanza dall'immagine dell'oggetto (ovvero dove posizioniamo il sensore per mettere a fuoco correttamente). Considera l'idea di mantenere s fisso ma di cambiare la lunghezza focale e di cambiare la distanza dell'oggetto per mantenere la messa a fuoco. la risposta di mattdm spiega efficacemente che la variazione dell'ingrandimento è il rapporto tra le distanze degli oggetti, quindi ci interessa

Pertanto, anche con il nostro obiettivo ideale, non otteniamo perfetto rapporto lineare tra il rapporto di ingrandimento e il rapporto di focale: c'è il termine di correzione tra parentesi. E in effetti ci sono termini di errore di ordine superiore perché di solito teniamo la fotocamera fissa e spostiamo l'obiettivo, quindi dovrebbe essere s + o che teniamo fisso anziché s .

Per scopi pratici, la distanza dal soggetto è solitamente molto maggiore della lunghezza focale. Per esempio. nella fotografia di strada potresti utilizzare un obiettivo da 50 mm o 100 mm per fotografare soggetti a 5 mo 10 m, quindi l'errore sarebbe nell'ordine dell'1%. È molto più significativo nella fotografia macro, dove potresti utilizzare un obiettivo da 100 mm con una distanza del soggetto di 300 mm.

In sintesi, anche idealizzando la situazione troviamo che la relazione non è esatta.

Tutto dipende da alcune definizioni e condizioni.

• La prima è la lunghezza focale. La lunghezza focale di molti obiettivi, se non della maggior parte, viene arrotondata per eccesso o per difetto alla lunghezza focale "standard" più vicina. Un obiettivo con una lunghezza focale effettiva di 53,78 mm sarà probabilmente etichettato come obiettivo da 55 mm. Un obiettivo con una lunghezza focale effettiva di 37,2 mm sarà probabilmente etichettato come un obiettivo da 35 mm. I teleobiettivi tendono quasi sempre ad arrotondare, in particolare gli obiettivi zoom. Il tuo obiettivo zoom 70-300 mm è probabilmente più vicino a essere effettivamente un obiettivo 78-287 mm o qualcosa di simile. Le lunghezze focali comuni designate dagli obiettivi includono 20 mm, 24 mm, 28 mm, 35 mm, 40 mm, 50 mm, 70 mm, 85 mm, ecc. Gli obiettivi che rientrano negli spazi tra questi numeri sono solitamente arrotondati a quello più vicino (in qualsiasi direzione il produttore vendere più lenti). Gli obiettivi inferiori a circa 18 mm sembrano generalmente essere arrotondati per difetto all'intero più vicino. Un obiettivo con una lunghezza focale effettiva di 12,6 mm sarà quasi sempre commercializzato come obiettivo da 12 mm. E sebbene ci siano obiettivi da 17 mm, 16 mm, 15 mm, 14 mm, 12 mm, 11 mm, 10 mm, ecc., Non sono sicuro di aver mai visto un obiettivo commercializzato come un 13 mm. Nella cultura occidentale 13 è considerato un numero sfortunato.
• La lunghezza focale degli obiettivi viene misurata quando sono a fuoco all'infinito. Quando la maggior parte degli obiettivi zoom è messa a fuoco più da vicino, tende ad aumentare l'angolo di campo che ha l'effetto di ridurre l'ingrandimento della lente. Le lenti prime, d'altra parte, di solito riducono il campo visivo poiché sono focalizzate più vicino, il che aumenta l'ingrandimento dell'obiettivo e riduce il campo visivo. Questo si chiama respiro focalizzato . Può essere corretto nel design dell'obiettivo, ma così facendo aumenta il costo dell'obiettivo. Alcuni teleobiettivi zoom possono essere famosi per questo. L'AF-S 70-200mm f / 2.8G VR II di Nikon è uno di questi. Alla massima zoom (contrassegnata 200mm) e la distanza minima di messa a fuoco del campo visivo proiettato su un sensore full frame è equivalente a una lunghezza focale di circa 134 millimetri solo! L'ultimo AF-S 70-200mm f / 2.8 FL VR di Nikon fa molto meglio in questo senso. Canon EF 70-200mm f / 2.8 L IS II respira verso l'esterno come un obiettivo primario e dà circa un 230 millimetri FOV a MFD paragonato a destra a 200mm a fuoco all'infinito. Gli obiettivi cinematografici tendono a correggere più o meno completamente la respirazione della messa a fuoco e i loro prezzi che possono essere circa 5-10 volte il costo delle loro controparti non cinematografiche lo riflettono. Un obiettivo macro in grado di proiettare un'immagine 1: 1 sul sensore (l'immagine proiettata sul sensore ha le stesse dimensioni dell'oggetto da riprendere) ha un campo visivo a 1: 1 che è la metà del suo campo visivo quando messo a fuoco all'infinito.
• due volte più grande è un po 'nebulosa Vuoi dire due volte più grande in termini di superficie totale delle coperture oggetto sul sensore (un obiettivo con La lunghezza focale 1.4X dovrebbe teoricamente farlo)? O intendi due volte più alto e due volte più largo, il che darebbe al soggetto quattro volte l'area sul sensore? Se intendi misurazioni lineari, un obiettivo da 200 mm messo a fuoco all'infinito dovrebbe far sembrare un soggetto all'infinito due volte più alto e largo di quanto un obiettivo da 100 mm messo a fuoco all'infinito farebbe sembrare un soggetto all'infinito.

Quindi, in teoria, un obiettivo con una lunghezza focale doppia dovrebbe proiettare un'immagine sul sensore che è molto vicina al doppio in modo lineare rispetto a un altro obiettivo.

Ma è pratico, soprattutto con obiettivi di livello consumer o persino zoom professionali, raramente funziona in questo modo con un certo grado di precisione.

Prendiamo ad esempio un tipico obiettivo macro da 100 mm e la citazione precedente Zoom 70-200 mm Nikon. Se posizioniamo il soggetto a 55 pollici (l'MFD del 70-200) l'obiettivo Macro sarà a circa 5X il suo MFD. L'obiettivo Macro avrà un campo visivo leggermente inferiore alla sua lunghezza focale nominale di 100 mm quando messo a fuoco all'infinito. Lo chiameremo 105mm. L'obiettivo zoom impostato a 200 mm e messo a fuoco su MFD, d'altra parte, avrà solo un FoV di circa un obiettivo 134 mm messo a fuoco all'infinito. Pertanto, l'ingrandimento fornito dal teleobiettivo da 200 mm sarà solo di circa 1,28 volte l'ingrandimento fornito dal Macro Prime da 100 mm!

Quanto sopra è, certamente, un esempio estremo. Ma non è così lontano dalla realtà di molti teleobiettivi zoom rispetto agli obiettivi fissi che tendono a respirare molto meno.

"Ero giunto alla conclusione che se un obiettivo ha il doppio della lunghezza focale di un altro, significa che tutto sembra due volte più grande". È corretto ottenere una A.

Innanzitutto lascia stabiliamo ciò che è "normale" per la nostra fotocamera in relazione alla lunghezza focale. "Normale" è un obiettivo che immagini simili all'esperienza umana. La vista prodotta da un obiettivo della fotocamera è definita "normale" quando la sua lunghezza focale corrisponde approssimativamente alla misura da angolo ad angolo delle dimensioni del formato. Ad esempio, una fotocamera a pellicola 35 mm full frame e la sua controparte digitale full frame (FX) misurano 24 mm di altezza per 36 mm di lunghezza. La misura diagonale di questo rettangolo è 43 ¼ mm. Se fossimo per montare un obiettivo con questa lunghezza focale, la vista fornita è definita "normale". Poiché questo valore è alquanto insolito, l'industria ha scelto di arrotondare questo valore a 50 mm.

Considerando anche il Formato DX (digitale compatto), le misure sono 16 mm di altezza per 24 mm di lunghezza. La misura diagonale arriva a 30 mm. A 30 mm su un DX offre una visualizzazione "normale".

OK, cos'è il grandangolo? Tecnicamente è una lente più corta del normale. Considero un obiettivo che è il 70% del "normale" o più corto per essere nel regno del grandangolo. Per il DX, è 35 mm o più corto. Per l'FX, 20 mm o meno. E il teleobiettivo? Questo è il 200% di "normale". Per l'FX, è 100 mm o più e per il DX, è 60 mm o più.

Diamo un'occhiata a cosa succede all'angolo di campo quando montiamo varie lunghezze focali su un formato DX:

30 mm "normale" = angolo di campo di 45 ° tenuto in orizzontale.

Molto spesso l'angolo di visuale citato è preso da un angolo all'altro (diagonale) = 52 °

Montare un 20 mm e l'angolo di visuale orizzontale è di 62 ° e la diagonale di 72 °.

Montare un 10 mm e l'orizzontale = 100 ° e la diagonale = 111 °

Spero che questo aiuti.

La cosiddetta funzione di mappatura prospettica è altezza dell'immagine = lunghezza focale * tan (metà campo visivo) . Se aggiusti l'altezza dell'immagine, ad es. 21,64 mm per il pieno formato, puoi risolvere il campo visivo di qualsiasi lunghezza focale.

Questa è una funzione non lineare, quindi se avessi ad es. un obiettivo da 1000 mm e un obiettivo da 2000 mm, il rapporto dei campi visivi sarebbe diverso ad es. un obiettivo da 10 mm e un obiettivo da 20 mm.